In March, I applied for an Innovation Teaching Grant through the Pearland ISD Education Foundation. The project is described below.
Project Summary
This project will provide the hardware required for real-time data collection by students working in small groups to support three Algebra 2 standards. Real time data collection and analysis provides the tools to allow students to focus on the collected data and provides the foundation for application of the learning from the Algebra 2 curriculum to Science classes.
Purpose
There are three Algebra 2 standards that apply to data collection:
1. Predict and make decisions and critical judgments from a given set of data using linear, quadratic, and exponential models.
2. Analyze data to select the appropriate model from among linear, quadratic, and exponential models.
3. Use regression methods available through technology to write a linear function, a quadratic function, and an exponential function from a given set of data.
The math department currently has a limited set of hardware which has been used for data collection to support these standards. With limited equipment, the data collection must be performed by the teacher with the resulting data supplied to the students for analysis.
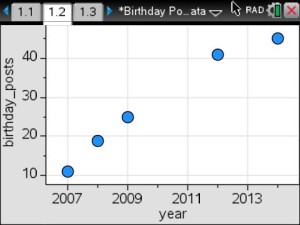
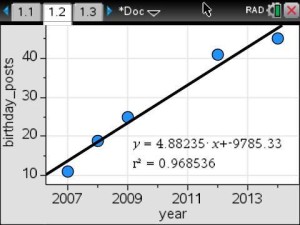
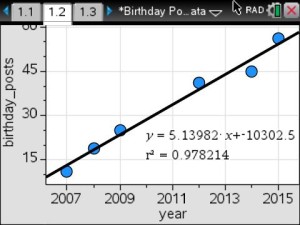
The purpose of the data collection project is to have students work in small groups to collect their own data, analyze and interpret the data, and predict and make decisions based on the appropriate model. In order for the students to perform the activities, we must have additional data collection equipment.
Objectives
By the end of the school year, all PAP Algebra 2 students will have completed at least three data collection activities (linear, quadratic, and exponential), working in small groups, utilizing the hardware supplied by this grant.
Project Description
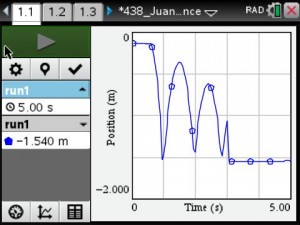
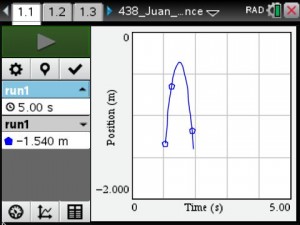
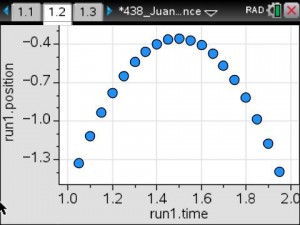
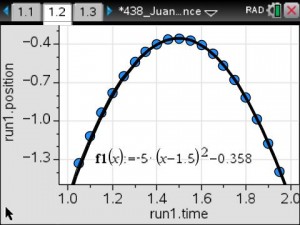
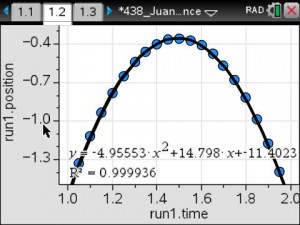
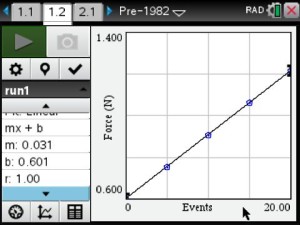
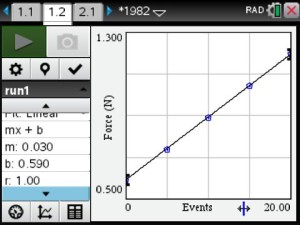
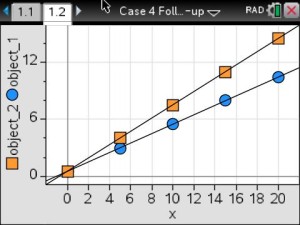
The teacher will use pre-made activities from TI’s Math Nspired or Vernier’s websites. Possible activities include That’s the Way the Ball Bounces – Height and Time for a Bouncing Ball, Chill Out: How Hot Objects Cool, and Making Cents of Math: Linear Relationships between Weight and Quantity.
Research suggests that real-time data collection seems to be the most effective way to connect a graph with real-world experiences. (Lapp, Douglas A., and Vivian Flora Cyrus. “Connecting Research to Teaching: Using Data-Collection Devices to Enhance Students’ Understanding.” Mathematics Teacher 93.6 (2000): 504-10. – National Council of Teachers of Mathematics. Web. 28 Feb. 2015.)
Automated data collection improves the accuracy of the data collected and allows students to focus on the positive educational impact of the development of the mathematical model rather than the methodology of the data collection.
Real-time data collection by the students will supply the foundation for the application of linear, quadratic and exponential models to the analysis of physical measurements made in science curriculum.
Project Evaluation
Students will complete the student pages available through the pre-made activities. The teacher will use the TI-Navigator to capture screen shots of the student’s data and to send quick polls to assess student’s understanding of concepts learned in each activity.
Budget
3 – Vernier EasyLink adapters – $175.50
3 – TI CBR2 motion sensors – $247.17
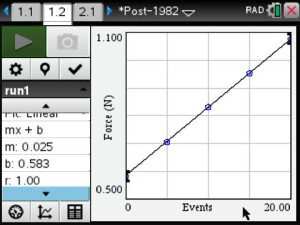
9 – Dual-range force sensors – $981.00
Other Funds Secured
For the students to perform their own data collection, working in small groups (4-5 students per group), there must be a total of 10 sets (5 sets per teacher) of data collection hardware.
The math department currently has:
2 – Vernier EasyLink adapters
2 – TI CBR2 motion sensors
6 – Temperature probes (5 personal property of one teacher)
1 – Dual-range force senors (personal property of one teacher)
Separate funding from a PTA grant has been secured for:
5 – Vernier EasyLink adapters – $292.50
5 – Temperature probes – $144.75
5 – TI CBR2 motion sensors – $411.95
Awarded May 28, 2015